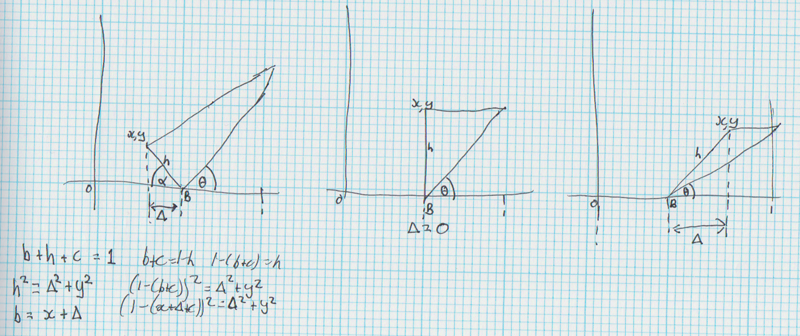As I was developing the ABC of the Sea App, which is an interactive picture-book based on a proof-of-concept Tara (my wife) made many years ago and did not publish, one of the early and obvious items on the checklist of cool things it should do is have a nice page curl transition when moving between pages. Initially I expected this to be easy – Apples Apps do this, iBooks on the iPad especially, so it’s built in, right?

Wrong. Well, mostly wrong. I quickly discovered that the only documented curling transition for a UIView goes up/down, not left/right. It’s the one that Maps uses. Some Googling then revealed that an undocumented transition did perform left/right curling. However, being undocumented means it’s not viable for an App Store submission. It may later acquire an official constant and become kosher, but not yet.

My quest continued. I came across a number of implementations but most of them were lame approximations of a proper page curl. The most promising one was by CodeFlakes that promised very good page-corner-tracking using touch events, so a user could drag the corner around, but it didn’t attempt to curl – it used shadows and gradients to fake the effect. When I queried this they said nobody had asked for real curling.

Page curl is really a page deformation

Then I came across this blog post by W. Dana Nuon: Implementing iBooks page curling using a conical deformation algorithm which was pretty close to what I wanted, except it used OpenGL – as yet an unknown quantity to me. I downloaded the code, examined it, tried to ignore the mathematics involved and eventually decided to use the concepts from it in my code. This took a while and I ended up with acceptable results, at least to be going on with. I parked the issue since I had working code and I wanted to focus on other aspects of the project.

Eventually I came back to it after I was working on some code to pre-render pages that touched the OpenGL code. As I dug in to it my confidence grew and then I finally decided to brave the math since I wanted to develop a touch-tracking mechanism, to drag the page around.

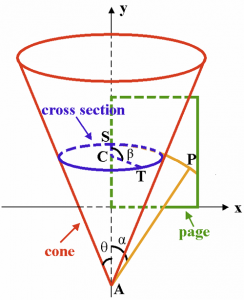
The basis of the conical deformation came from a research paper published by Xerox PARC on the topic where they used a cone with parameters that varied over the course of the transition as an approximation of a page turn. The model assumes a cone, apex-down, with a vertex running from that apex on the y-axis (that is, x=0). The y coordinate of the apex is a variable, A. The other cone parameter is the angle, θ, between the surface of the cone and a vertex that runs from the apex through the center of the cone. They then add a third parameter, ρ, which is the rotation of the entire page about the y-axis. The PDF from PARC linked above has a reasonably descriptive diagram showing this arrangement which I have shown here. Nuon then empirically determined a heuristic based on time t that varied these parameters to produce a reasonable animation.

The original algorithm for mapping a point onto the surface of a cone, from Nuon’s sample code and taken directly from the mechanism described by PARC, looked like this:

The short version of what this does is assume that the distance from the apex of the cone to the 2D location of a point on the flat page is the same as the distance from the apex to where that point would be when mapped onto the cone. Some simple geometry gives you a short cut to then work out the angle around the cone that this point ends up.

When I started to dissect this algorithm, ostensibly to invert the equations, I came across some significant hurdles. The most significant one was that the cone deformation, as implemented, had a serious limitation of where it would position the corner of the page in the view-port. There were two major elements to this limitation:

1. The entire page was mapped to a position on the cone. There were no flat parts. To get the corner of the page into some locations, you ended up either having the page curl back in on itself slightly or you ended up with a large z-component which looked odd.
2. The parameters necessary to achieve some corner locations required extreme values and these were hard to develop a heuristic for.

After messing around with a sheet of paper for 30 minutes and after examining some sketches of a page curl I decided I could overcome most of these limitations if I could introduce flat-parts into the deformation. In effect, I wanted to add an x-component to the position of the apex of the cone and limit how far around the cone a page would curl. It was time to dust off the trigonometry that I had not used in twenty years.

Moving the apex

Using my imagination, I called the new parameter B (meaning that {x,y} of the apex would be {B,A} in the code) and once I realized it was a small matter of offsetting in the right places and conditionally transforming a point, ended up with this:

The effect of this code is to provide a flat page prior to the cone, which starts at x=B. Experimentally I found that the useful range of θ was about 18 to 30 degrees. I then wrote some code to map an arbitrary {x,y} point to the parameters for the curl and, though it was better than for the stock deformation, it was not perfect:

In particular, though the corner does move with the touch location, it’s not directly under it. I decided this was a matter of refinement but, more pressing, there was still a significant limitation to where it could place the corner of the page – it needed to flatten the page after the cone in order to reach more places.

This proved to be rather tricky. In order to do this, you need to transform the points relative to the last position they would have had on the cone. All of the math discovered this location in terms of the distance from the apex, which is a function of the original 2D position. Not something that can be easily inferred from an arbitrary point.

Would a tube work?

Instead of going down a path of nasty trigonometry, I decided to attack it from a different angle. Instead of a cone, why not a cylinder whose point of rotation was freely movable? The geometry involved would be much simpler – and it should be pretty easy to reverse, too. I went and found a kitchen paper-towel tube and a sheet of paper and convinced myself it was a reasonable model.

Cylinders are pretty easy objects to draw in 3D – it’s just a 2D circle, in our case with radius C, that you transform into 3D and then extrude. A bit trickier is using this simple model and wrapping a page around it – this is because the page doesn’t simply follow the cylinder around in a circle, it’s an ellipse and for a given plane in the 2D page, one complete revolution around the tube does not end up at the same point it started – just wrap a page around a tube to see. The page travels up the tube when it’s at an angle.

Initially I thought that the angle formed by the path leading into the cylinder and the path leading out was 2θ but that ended up being too simplistic, not least because I inadvertently changed the meaning of θ to be the angle between the x-axis and the vertex that ran along the face of the cylinder at z=0. What I ended up with was .

The code to perform this deformation ended up reasonably clean, if not as simple as the conical one looked:

Now this is not perfect either, in particular, for values of approaching there is a small tendency for the page to curve below the y-axis a little. This I hope to remedy later. It’s also straightforward to curl from a different corner, or even an edge, thanks to the complete flexibility of the rotation point of the cylinder. Significantly, however, the logic to map an {x,y} location to deformation parameters proved, if not straight forward then very achievable.

But can you touch it?

By looking at a sketch of three phases of the cylindrical deformation it became clear that there was a single equation that could involve all the parameters to hand. I called the distance along the bottom edge of the page that was after the cylinder h, the distance along that edge that was wrapped around the cylinder c and the distance along the bottom edge, on the x-axis, that runs from where the page leaves the x-axis back to the x-coordinate of the corner of the page being dragged Δ.

With this, it was apparent that , that and that . With substitution, you end up with:

and you know what? It works. Calculating θ was simple Pythagoras and I ended up with:

And there we have it. There are further refinements to make – for θ approaching  our OpenGL vertices have a problem coping and the edge of the curl looks ragged. There’s the problem noted above with the curl dipping below the x-axis. And for larger values of c the touch tracking code loses accuracy. But these can all be worked on.